Starten met beleggen: welke boeken zijn aan te raden?
TIP
Re: Starten met beleggen: welke boeken zijn aan te raden?
Voor het geval het iemand met mij eens kan zijn (maar anders ook) :
De beurs en beleggen in aandelen of zelfs fondsen is iets waar veel geluk en toeval mee gemoeid is.
Minder dan Lotto maar eerder zoiets als de paardenkoersen, waar enige voorkennis van nut kan zijn.
Maar om daar echt een boek over te lezen en schrijven... pffffffff...
Ik betwijfel dat een boek je kan leren gokken.
De beurs en beleggen in aandelen of zelfs fondsen is iets waar veel geluk en toeval mee gemoeid is.
Minder dan Lotto maar eerder zoiets als de paardenkoersen, waar enige voorkennis van nut kan zijn.
Maar om daar echt een boek over te lezen en schrijven... pffffffff...
Ik betwijfel dat een boek je kan leren gokken.
Opinions are like assholes. Everybody has one and they all stink.
Re: Starten met beleggen: welke boeken zijn aan te raden?
Jawel hoor.

Maar ik ben het niet met je eens dat de beurs een casino is.

Maar ik ben het niet met je eens dat de beurs een casino is.
Re: Starten met beleggen: welke boeken zijn aan te raden?
De beurs is zeker geen casino.
Maar het blijft ook wel wat gokken zoals in een casino Ondanks je ook wel zekerheden hebt zoals een Microsoft, PepsiCo,.. Ga je niet meer rijk van worden, maar moet je wel een spaarrekening mee kunnen verslaan.
Ondanks je ook wel zekerheden hebt zoals een Microsoft, PepsiCo,.. Ga je niet meer rijk van worden, maar moet je wel een spaarrekening mee kunnen verslaan.
Maar het blijft ook wel wat gokken zoals in een casino
Re: Starten met beleggen: welke boeken zijn aan te raden?
Er is in mijn ogen een veel betere reden om te spreiden dan wat jullie aanhalen en dat is om de effectentaks te vermijden .vortex schreef: ↑2 februari 2024, 18:32LOL Ga eerst maar eens het verschil tussen kans (probability) en risico leren, je slaat een en ander door elkaarhuisjetuintjefiets schreef: ↑2 februari 2024, 18:00
Jij kunt niet rekenen, makker. Het is altijd cijfers en rekenen. Wie dat niet kan, is zeer kwetsbaar om verkeerde meningen te hebben.
Ik heb 1 miljoen euro (hypothetisch).
Nemen we dat het risico om alles bij één broker te verliezen 0,001% is per jaar. Hoe groot het echt is, heeft geen belang. Het verandert de redenering en de resultaten niet.
Aangezien we enkel verlies door fraude bij één broker als verliesmogelijkheid nemen, kunnen we stellen dat de risico's voor één broker onafhankelijk zijn van andere brokers.
Als ik alles bij 1 broker zet, dan is mijn verwachte verlies per jaar: 0,001% × 1 miljoen.
Als ik deel over 2 brokers, dan is mijn verwachte verlies per jaar: 0,001% × 500.000 + 0,001% × 500.000.
Dat is inderdaad hetzelfde verwachte verlies. Tot hier heb je gelijk.
Jammer dat je hier gestopt bent met denken.
Let goed op: hier volgt de reden dat splitsen over 2 brokers zinvol is
Wat is de kans dat ik effectief mijn miljoen kwijt raak in een jaar?
Staat alles bij 1 broker, dan is de kans: 0,001%.
Staat alles bij 2 brokers, dan is de kans 0,001% × 0,001% (onafhankelijke kansen) = 0,000001%.
Voilà. Cijfers en rekenen. En ook wat nadenken
Twee kansen op een half miljoen is een even groot risico dan één kans op een miljoen.
Nu het overzetten niet meer aanzien word als belastingfraude als je de term veiligheid noemt als reden.
Maar denk dat vanaf nu bijna niemand deze nog zal betalen tenzij je geblokkeerd zit .
Re: Starten met beleggen: welke boeken zijn aan te raden?
Daar ben ik het nu volledig mee oneens het zijn juist de gevestigde bedrijven die je rijk kunnen maken op de beurs maar de mensen hebben het geduld niet en zien 10 jaar als een lange periode .
De laatste jaren presteert groei beter maar de 50 jaar daarvoor is het altijd anders geweest .
Zekerheid en tijd dat is het enige dat nodig is om een fortuin te maken op de beurs .
En aandelen zoals Tesla , Amazon ed geven u niet die zekerheid .
Zo'n aandelen moet iemand dan ook aanschouwen als aanvulling maar nooit als kern .
PEP heeft trouwens de laatste 10 jaar een total return van 11,22 % de benchmark S&P 500 had maar 10,96 % in die periode .
Traag maar zeker maar deze lessen moeten geleerd worden en dit leergeld zorg er veel voor dat mensen nooit geen fortuin zullen verdienen op de beurs .
Bijna iedereen die zijn fortuin heeft gemaakt door beleggen heeft dit zo gedaan .
Je moet het licht niet opnieuw uitvinden .
Maar soms duurt het lang voor mensen dit beseffen .
Re: Starten met beleggen: welke boeken zijn aan te raden?
Volledig mee eens.
En het is geen gok om mee te gaan met holdings in goede papieren zoaks Berkshire H, Investor AB, Brederode of ETF's van de S&P 500 of de wereldindex.
Ik denk dat je ze kunt beschouwen als een buy and "forget". => "forget" blijft tussen aanhalingstekens!
Re: Starten met beleggen: welke boeken zijn aan te raden?
Stel dat de kans op faillissement van een broker 1/1.000.000 is. Laten we deze kans aanduiden als P(F).vortex schreef: ↑2 februari 2024, 18:32LOL Ga eerst maar eens het verschil tussen kans (probability) en risico leren, je slaat een en ander door elkaarhuisjetuintjefiets schreef: ↑2 februari 2024, 18:00
Jij kunt niet rekenen, makker. Het is altijd cijfers en rekenen. Wie dat niet kan, is zeer kwetsbaar om verkeerde meningen te hebben.
Ik heb 1 miljoen euro (hypothetisch).
Nemen we dat het risico om alles bij één broker te verliezen 0,001% is per jaar. Hoe groot het echt is, heeft geen belang. Het verandert de redenering en de resultaten niet.
Aangezien we enkel verlies door fraude bij één broker als verliesmogelijkheid nemen, kunnen we stellen dat de risico's voor één broker onafhankelijk zijn van andere brokers.
Als ik alles bij 1 broker zet, dan is mijn verwachte verlies per jaar: 0,001% × 1 miljoen.
Als ik deel over 2 brokers, dan is mijn verwachte verlies per jaar: 0,001% × 500.000 + 0,001% × 500.000.
Dat is inderdaad hetzelfde verwachte verlies. Tot hier heb je gelijk.
Jammer dat je hier gestopt bent met denken.
Let goed op: hier volgt de reden dat splitsen over 2 brokers zinvol is
Wat is de kans dat ik effectief mijn miljoen kwijt raak in een jaar?
Staat alles bij 1 broker, dan is de kans: 0,001%.
Staat alles bij 2 brokers, dan is de kans 0,001% × 0,001% (onafhankelijke kansen) = 0,000001%.
Voilà. Cijfers en rekenen. En ook wat nadenken
Twee kansen op een half miljoen is een even groot risico dan één kans op een miljoen.
Om 1.000.000€ te verliezen moeten beide brokers failliet gaan. De kans hierop is het product van de afzonderlijke kansen:
P(1.000.000€ verlies) = P(F1 en F2) = P(F1) x P(F2) = (1/1.000.000)*(1/1.OOO.OOO) = 1/1.000.000.000.000 = 0.0000000001%
Wat is de kans om 500.000€ te verliezen?
Om 500.000€ te verliezen zijn er twee mogelijke scenario's:
- broker 1 failliet en broker 2 niet failliet
- broker 1 niet failliet en broker 2 failliet
De kansen op deze afzonderlijke scenario's zijn het product van de individuele kansen:
P(500.000€ verlies) = P(F1 en niet F2) + P(niet F1 en F2)
= P(F1) x P(niet F2) + P(niet F1) x P(F2)
= (1/1000000)x(1 - 1/1000000) + (1 - 1/1000000)x(1/1000000)
= (2/1000000) x (1 - 1/1000000)
= 0.0002%
Re: Starten met beleggen: welke boeken zijn aan te raden?
Jaja, allemaal goed en wel maar naast de kwestie. Huistuintje had het over risico, niet over kansen, hij poste er zelfs een risico matrix bij die hij vervolgens verkeerd interpreteerde. Het verschil tussen probability (kans) en risico wordt precies toch niet zo goed begrepen
-
huisjetuintjefiets
- Verbannen Gebruiker

- Berichten: 1642
- Lid geworden op: 20 mar 2022
Re: Starten met beleggen: welke boeken zijn aan te raden?
****** AANVULLING ****** Ik zie net dat Philippe1 dezelfde berekeningen als mij heeft gemaakt
Punt 1: het verschil tussen "verwacht verlies" en "totaal mogelijk verlies".
"Risico" is niet zoals "lengte" of "gewicht". De laatste zijn eenduidig bepaald (al kun je ze wel in andere eenheden uitdrukken: mm, m, km, ...).
"Risico" is niet zo. Je kunt verschillende maten van risico bekijken:
- verwacht verlies (wat ik gebruikte; dat is een veelgebruikte maat om risico uit te drukken)
- het totaal mogelijke verlies: hoeveel kun je maximaal verliezen. Bij aandelen, obligaties, en zelfs spaarboekjes met staatsgarantie tot 100.000: je kunt 100% kwijt zijn.
- ...
"Verwacht verlies" kun je zelfs gebruiken om een bedrag te plakken op reputatierisico, politiek risico, ...
"Totaal mogelijk verlies ook" kun je ook hiervoor gebruiken. Je hebt een fabriek in Rusland. Door het (reële) politieke risico kun je je hele fabriek kwijtraken
Punt 2: correct rekenen
Wat met de bewering: Twee kansen op een half miljoen is een even groot risico dan één kans op een miljoen.
(Dit in de context: heeft het vanuit risicostandpunt zin om 1 miljoen bij een broker te splitsen over 2 brokers: 500.000 bij elk van de 2)
Ik heb al hierboven stap voor stap uitgelegd dat de kans om 1 miljoen te verliezen in geval van splitsing het kwadraat is van de kans bij niet splitsing.
Vb 0,001% kwadraat tov 0,001%.
En, zoals ik eerder heb uitgelegd. Het verwachte verlies met of zonder splitsing is inderdaad gelijk:
0,001% × 1 miljoen = 0,001% × 500.000 + 0,001% × 500.000.
Ik had hierboven al uitgelegd dat we het op dit punt eens waren. als we inderdaad verwacht verlies gebruiken als maatstaf.
Maar als we jouw bewering letterlijk nemen:
Twee kansen op een half miljoen is een even groot risico dan één kans op een miljoen.
dan is dat een bewering die totaal verkeerd is.
Bij splitsing zijn er inderdaad 2 kansen om een half miljoen te verliezen: 0,001% × 500.000.
Je telt dat gewoon bij elkaar op en komt zo tot jouw totaal verkeerde conclusie.
De juiste werkwijze is: bij splitsing over 2 brokers, kun je enkel 1 miljoen verliezen als je je geld bij beide brokers kwijtraakt.
En om dat te berekenen, moet je de kansen vermenigvuldigen en niet optellen.
En dus 0,001% vermenigvuldigen met 0,001% om de kans op 1 miljoen verlies te berekenen.
Punt 3: het gezond verstand zet jou op het verkeerde been
Praktisch iedereen voelt aan: ja, door grootschalige fraude bij een broker kan ik al mijn geld kwijtraken, ook al is de kans zeer klein !!!!!
Zonder splitsing kan ik 1 miljoen kwijtraken bij 1 broker
Bij splitsing: een half miljoen bij 1 broker.
Maar wacht eens: als ik mijn geld splits over 2 brokers, dan loop ik 2 keer de kans om te verliezen !!!!!! 2 keer 500.000 kunnen verliezen, is gelijk aan 1 miljoen kunnen verliezen.
En dus heeft splitsing geen zin (zegt het gezond verstand).
De enige correcte redenering staat hierboven: 0,001% × 0,001% is de kans om 1 miljoen te verliezen.
Om hetzelfde anders te zien: wat is de kans dat ik bij splitsing 500.000 verlies?
Er zijn 2 mogelijkheden: ik verlies mijn geld bij de ene broker OF ik verlies mijn geld bij de tweede broker.
Hier moet je de kansen wel optellen.
De kans om 500.000 te verliezen is 0,001% + 0,001%.
Die kans is dubbel zo groot als de kans om 1 miljoen te verliezen zonder splitsing maar 0,001% of 0,002% zijn qua grootteorde gelijk, heel anders dan het verschil tussen 0,001% en 0,001% × 0,001%.
Samenvatting
Zonder splitsing: 0,001% kans om 1 miljoen te verliezen.
Bij splitsing:
- 0,002% kans om exact 500.000 te verliezen
- 0,000001% kans om 1 miljoen te verliezen
- 0,002001% kans om 500.000 of 1 miljoen te verliezen
Voor mij is het duidelijk wat het beste resultaat geeft: splitsen. Ik verlies liever 500.000 dan 1 miljoen.
-
huisjetuintjefiets
- Verbannen Gebruiker

- Berichten: 1642
- Lid geworden op: 20 mar 2022
Re: Starten met beleggen: welke boeken zijn aan te raden?
Vortex zal het niet graag zien: hij is een grote fan van jou. Hij beweert dat het risico niet verminderd wordt door te splitsen tussen brokers. En dus verhoogt de veiligheid niet
Wie heeft gelijk:
- jij en
- Philippe1 en
- de fiscus en
- ik
Of:
- Vortex
-
huisjetuintjefiets
- Verbannen Gebruiker

- Berichten: 1642
- Lid geworden op: 20 mar 2022
Re: Starten met beleggen: welke boeken zijn aan te raden?
Zeer laag van jou, maar we kennen jou ondertussenvortex schreef: ↑4 februari 2024, 10:39Jaja, allemaal goed en wel maar naast de kwestie. Huistuintje had het over risico, niet over kansen, hij poste er zelfs een risico matrix bij die hij vervolgens verkeerd interpreteerde. Het verschil tussen probability (kans) en risico wordt precies toch niet zo goed begrepen
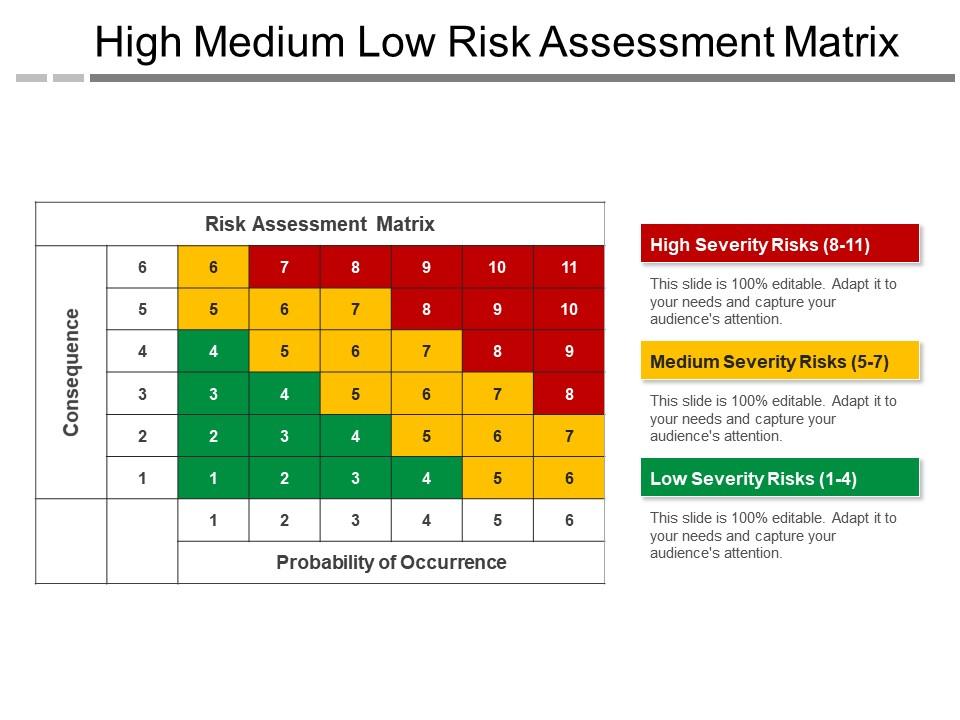
Die matrix heb ik gebruikt om als huiswerk te laten inzien: het splitsen tussen brokers is mitigatie voor een risico waarvan de probabiliteit laag is, maar de impact hoog
En dat staat linksboven in de matrix
Maar jij snapt dus niet dat het bij risico niet alleen gaat om het verlies dat je kunt lijden, maar ook over de kans dat je dit verlies lijdt
Re: Starten met beleggen: welke boeken zijn aan te raden?
Philippe en vortex hebben gelijk, zij gebruiken de term kans en risico correct, mijn vriend lop krijgt gelijk en jij snap het verschil tussen kans en risico nog altijd niethuisjetuintjefiets schreef: ↑4 februari 2024, 11:09 Vortex zal het niet graag zien: hij is een grote fan van jou. Hij beweert dat het risico niet verminderd wordt door te splitsen tussen brokers. En dus verhoogt de veiligheid niet
Wie heeft gelijk:
- jij en
- Philippe1 en
- de fiscus en
- ik
Of:
- Vortex

Re: Starten met beleggen: welke boeken zijn aan te raden?
Maak dan je eigen huiswerk eens en gebruik dan die matrix héhuisjetuintjefiets schreef: ↑4 februari 2024, 11:10
Zeer laag van jou, maar we kennen jou ondertussen. Insinueren, verdachtmakingen, leugens, ... dat is jouw arsenaal.
Die matrix heb ik gebruikt om als huiswerk te laten inzien: het splitsen tussen brokers is mitigatie voor een risico waarvan de probabiliteit laag is, maar de impact hoog
En dat staat linksboven in de matrix
scenario 1 links boven consequence 6, probability 1 => risico 6
scenario 2 consequence 5, probability 2 => risico nog steeds 6
-
huisjetuintjefiets
- Verbannen Gebruiker

- Berichten: 1642
- Lid geworden op: 20 mar 2022
Re: Starten met beleggen: welke boeken zijn aan te raden?
Goed dat je de matrix aanhaaltvortex schreef: ↑4 februari 2024, 11:29Maak dan je eigen huiswerk eens en gebruik dan die matrix héhuisjetuintjefiets schreef: ↑4 februari 2024, 11:10
Zeer laag van jou, maar we kennen jou ondertussen. Insinueren, verdachtmakingen, leugens, ... dat is jouw arsenaal.
Die matrix heb ik gebruikt om als huiswerk te laten inzien: het splitsen tussen brokers is mitigatie voor een risico waarvan de probabiliteit laag is, maar de impact hoog
En dat staat linksboven in de matrix

scenario 1 links boven consequence 6, probability 1 => risico 6
scenario 2 consequence 5, probability 2 => risico nog steeds 6

Nu begin je zelf over kans en risico
Alleen jammer dat je de matrix wel theoretisch snapt, maar faalt bij de toepassing in de praktijk.
Kans op 1 miljoen verlies
Geen splitsing broker:
- risico linksboven, 6. Kans 0,001% op verlies 1 miljoen
Wel splitsing broker:
- risici inderdaad ook linksboven, maar ongelooflijk nog meer naar links: 0,001% × 0,001% kans verlies op 1.000.000
Als je redenering is: het staat in hetzelfde hokje, dus krijgt het dezelfde score, dan heb je gelijk.
Zet je verstand open en verfijn de matrix.
Van 0,000001% tot 0,001%. Dat is een factor 1000.
Als je dat in een zinvolle matrix zet, dan heb je 1000 hokjes van 0,000001% tot 0,001%.
Als je dan koppig volhoudt, en in al die hokjes 6 zet, dan zijn we uitgepraat. Maar dan zeg je dat 0,001% hetzelfde is 0,000001%.
Je moet wel weten waarmee je bezig bent om deze stap te kunnen zetten. Als je blind theorie toepast, kom je nergens.
Risico van minstens 500.000 verlies
Zonder splitsing: de kans zal kleiner zijn om 500.000 te verliezen dan om 1 miljoen te verliezen. Kans op 500.000 verlies dus kleiner dan 0,001%.
Met splitsing: 0,002% kans om minstens 500.000 te verliezen (ik verwaarloos de 0,000001%)
In de matrix zal dit dichter bij elkaar liggen dan de kans op 1 miljoen verlies (0,002% tov iets dat iets kleiner is dan 0,001%). Relatief veel dichter bij elkaar dan 0,001% en 0,000001%.
Het punt om te splitsen is die 1 miljoen bij 1 broker. Dat is mijn hele bezit (de hypothetische aanname bij het begin).
Ik wil het mogelijk verlies van mijn volledige bezit zo klein mogelijk maken, ook al loop ik iets groter risico om 500.000 te verliezen.
Re: Starten met beleggen: welke boeken zijn aan te raden?
Allez we zullen daar eens een zinvolle matrix van makenhuisjetuintjefiets schreef: ↑4 februari 2024, 12:05
Goed dat je de matrix aanhaalt
Nu begin je zelf over kans en risico
Alleen jammer dat je de matrix wel theoretisch snapt, maar faalt bij de toepassing in de praktijk.
Kans op 1 miljoen verlies
Geen splitsing broker:
- risico linksboven, 6. Kans 0,001% op verlies 1 miljoen
Wel splitsing broker:
- risici inderdaad ook linksboven, maar ongelooflijk nog meer naar links: 0,001% × 0,001% kans verlies op 1.000.000
Als je redenering is: het staat in hetzelfde hokje, dus krijgt het dezelfde score, dan heb je gelijk.
Zet je verstand open en verfijn de matrix.
Van 0,000001% tot 0,001%. Dat is een factor 1000.
Als je dat in een zinvolle matrix zet, dan heb je 1000 hokjes van 0,000001% tot 0,001%.
BTW; zo een matrix is zoals al eens eerder gezegd logaritmisch, elk punt stijging is een verdubbeling.
Scenario 1) probability 0,001% op een verlies van 1.000.000 consequence => risico score 6
Scenario 2) probability 0,002% op een verlies van 500.000 consequence => risico score 6
[/quote]
Laatst gewijzigd door vortex op 4 februari 2024, 13:25, 1 keer totaal gewijzigd.


